ত্রিমাত্রিক ভেক্টর

ত্রিমাত্রিক ভেক্টর এর মান বের করার জন্য আমরা একটা ত্রিমাত্রিক স্থানাংক ব্যবস্থা নিয়ে চিন্তা করি, যেখানে P নামক একটা বিন্দুর অবস্থান P (x, y, z). একইসাথে X, Y এবং Z axis বরাবর A, B এবং C বিন্দুর দুরত্ব হচ্ছে যথাক্রমে x, y, z.

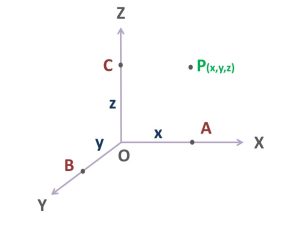
মূল বিন্দু O থেকে P এর দিকে ভেক্টর হচ্ছে OP. যদি OP ভেক্টরের মান বের করতে চাই তবে ভেক্টরের উপর থেকে তীর চিহ্ন সরিয়ে দিতে হবে, অর্থাৎ- OP

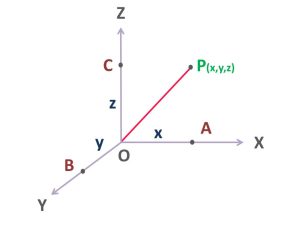
এখানে OP হচ্ছে একটি রেখা, যেটি ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থায় অবস্থান করছে। P বিন্দু থেকে যদি একটা লম্ব টানি তবে সেটি X-Y তলের ওপর Q বিন্দুতে অবস্থান করবে। যদি Q এবং O বিন্দুকে যুক্ত করি তবে OPQ একটি সমকোণী ত্রিভুজ পাবো, যেখানে OP হচ্ছে অতিভুজ, OQ হচ্ছে ভূমি এবং PQ হচ্ছে লম্ব।

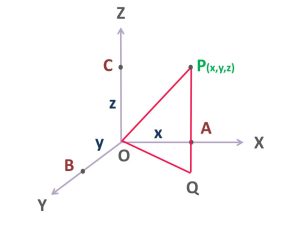
তাহলে পিথাগোরাসের সূত্র অনুসারে পাবো-

PO^2 = PQ^2 + OQ^2

or, PO = √(PQ^2 + OQ^2)

এখানে Z axis বরাবর PQ এর মান হচ্ছে z, কিন্তু আমরা OQ এর মান জানি না। যদি আমরা B এবং Q বিন্দু যোগ করি তবে খেয়াল করো OBQ এটি আরও একটি সমকোণী ত্রিভুজ তৈরি হবে-

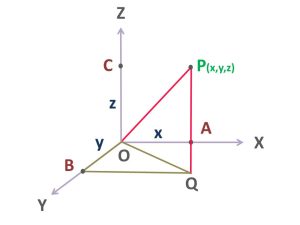
যেখানে পিথাগোরাসের সূত্র প্রয়োগ করলে পাবো-

OQ^2 = OB^2 + BQ^2

এখানে Y axis বরাবর OB এর মান হচ্ছে y, X axis বরাবর OA এর মান হচ্ছে x. তাহলে OP ভেক্টরের মান হবে-

OP = √(PQ^2 + OQ^2)

OP = √(PQ^2+ OB^2 + BQ^2)

তাহলে বলা যায় কোনো ত্রিমাত্রিক ভেক্টর এর মান হচ্ছে সেই ভেক্টরের স্থানাঙ্ক গুলো বর্গ করে তারপর তাদের যোগ করে এর উপর বর্গমূল বসিয়ে দেওয়া।