বোর পরমাণু মডেল

রাদারফোর্ডের পরমাণু মডেলে যখন কিছু সমস্যা ধরা পড়লো তখন বোর পরমাণু মডেলের আবির্ভাব ঘটে। বোর পরমাণু মডেল এর তিনটা প্রস্তাব আছে। এগুলো হলো-

১ম প্রস্তাব : শক্তিস্তর সম্পর্কিত

ইলেকট্রনগুলো পরমাণুতে নির্দিষ্ট কক্ষপথে থাকে এবং সেসময় ইলেকট্রন নির্দিষ্ট মানের কম পরিমাণ শক্তি শোষণ বা বিকিরণ করে না।

এর মানে হচ্ছে, কক্ষপথে থাকাকালীন সময় ইলেকট্রন নূন্যতম একটা শক্তি শোষণ বা বিকিরণ দুটোই করতে পারে কিন্তু সেই শক্তির পরিমাণটা নির্দিষ্ট থাকে। ধরা যাক একটা নির্দিষ্ট কক্ষপথে ঘুরতে থাকা ইলেকট্রনকে আমরা 10 J শক্তি দিলাম, কিন্তু সেটা কক্ষপথ থেকে বের হলো না। কিন্তু 15 J শক্তি দেওয়াতে সে কক্ষপথ থেকে বের হয়ে গেলো। তাই এই ইলেকট্রনটি 15 J এর কম শক্তি শোষণ করতে পারবে না। এটাই শক্তিস্তর সম্পর্কিত প্রস্তাব।

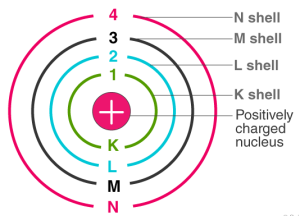
বোর পরমাণু মডেল এর এই প্রস্তাব অনুসারে, ইলেকট্রন পরমাণুতে নির্দিষ্ট কতগুলো কক্ষপথে থাকে। এই কক্ষপথ গুলোকে K, L, M, N বর্ণ দিয়ে কিংবা 1, 2, 3, 4 ইত্যাদি নাম্বার দিয়ে প্রকাশ করা হয় যেখানে ১ম কক্ষপথ বা শেলের নাম K।

২য় প্রস্তাব : কৌণিক ভরবেগ সম্পর্কিত

কোনো কক্ষপথে ঘূর্ণায়মান অবস্থায় ইলেকট্রনের একটা নির্দিষ্ট কৌণিক ভরবেগ থাকবে।

বোর পরমাণু মডেল এর এই প্রস্তাবের মানে হচ্ছে পরমাণুতে একেকটা কক্ষপথে থাকা একেকটা ইলেকট্রনের ভিন্ন ভিন্ন মানের কৌণিক ভরবেগ থাকবে। কৌণিক ভরবেগের সূত্র-

L = Iω

    = mr² (v / r)

    = mvr

যেখানে I = জড়তার ভ্রামক, r = কক্ষপথের ব্যাসার্ধ, h = প্লাংকের ধ্রুবক = 6.626 * 10^-34 Js, m = ইলেকট্রনের ভর, v = কক্ষপথে ইলেকট্রনের রৈখিক বেগ

আবার এখানে আরো একটা সম্পর্ক হচ্ছে L ∝ n, এর মানে কক্ষপথের সংখ্যা যত বাড়তে, কৌণিক ভরবেগের সংখ্যাও তত বাড়বে। তাহলে,

L ∝ n

or, L = n * constant

or, L= nh/2π

যেখানে h/2π হচ্ছে ধ্রুবকের মান।

৩য় প্রস্তাব : শক্তির বিকিরণ – শোষণ সম্পর্কিত

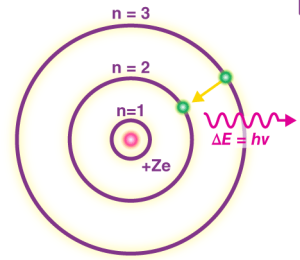
বোর পরমাণু মডেল অনুসারে ইলেকট্রন একটা নির্দিষ্ট পরিমাণ শক্তি শোষণ বা বিকিরণ করে অন্য কক্ষপথে যেতে পারে। এই শোষণ বা বিকিরণ করা শক্তির নির্দিষ্ট মানকে কোয়ান্টাম শক্তি বলে।

ইলেকট্রন যদি শক্তি শোষণ করে তবে সে নিচের কক্ষপথ থেকে উপরের কক্ষপথে যেতে পারবে। আর যদি সে শক্তি বিকিরণ করে বা ছেড়ে দেয়, তবে ইলেকট্রন উপরের কক্ষপথ থেকে নিচের কক্ষপথে নেমে আসবে।

এখন পরমাণুতে থাকা ইলেকট্রনকে বিভিন্ন উপায়ে শক্তি দেওয়া যায় তেমন তাপের মাধ্যমে, আলোর মাধ্যমে যেখানে শক্তিকে একটা তরঙ্গের আকারে পাঠাতে হয়। তাই এই শক্তির মান তরঙ্গের কম্পাংকের সমানুপাতিক হবে। অর্থাৎ-

E ∝ f

or, E = hf, যেখানে h হচ্ছে প্লাংকের ধ্রুবক।

or, E = hc / λ (কারণ v = fλ এবং c = আলোর বেগ)

কোয়ান্টাম শক্তি

এটি কোয়ান্টাম শক্তিকে অন্যভাবে লিখা যায়-

E = R_H‘ (1/n_i² – 1/n_f²)

এখানে, R_H‘ = রিডবার্গের ধ্রুবক (শক্তির ক্ষেত্রে) = 2.18 * 10^-18 J, n_i = আদি কক্ষপথ, n_f = শেষ কক্ষপথ।

এখানে E এর মান +ve কিংবা -ve দুটোই আসতে পারে। যখন n_i > n_f হবে তখন E = -ve মান আসবে। এর মানে ইলেকট্রনটি শক্তি বিকিরণ করেছে। আবার n_f > n_i হলে E = +ve মান আসবে। এর মানে ইলেকট্রনটি শক্তি শোষণ করেছে।

আবার, উপরের ফর্মুলাকে এভাবেও লিখা যায়-

E = hc / λ = R_H‘ (1/n_i² – 1/n_f²)

or, hc / λ = R_H‘ (1/n_i² – 1/n_f²)

or, 1 / λ = (R_H‘ / hc) * (1/n_i² – 1/n_f²)

or, 1 / λ = R_H * (1/n_i² – 1/n_f²)

এখানে, R_H = রিডবার্গের আরো একটা ধ্রুবক (তরঙ্গদৈর্ঘ্যের ক্ষেত্রে) = 109678 cm^-1

এবার আমরা তরঙ্গ সংখ্যা নিয়ে একটু জানি। প্রতি এক মিটার দৈর্ঘ্যে কয়টা তরঙ্গ আছে সেটার সংখ্যাটাই হচ্ছে তরঙ্গ সংখ্যা। একে v দিয়ে প্রকাশ করা হয়।

তাহলে, λ m দৈর্ঘ্য হচ্ছে 1 টি তরঙ্গের

1 m দৈর্ঘ্য হচ্ছে 1/λ টি তরঙ্গের

অর্থাৎ miu = 1/λ, এর একক m^-1

তাহলে আমাদের সূত্রটি হবে,

v = (R_H‘ / hc) * (1/n_i² – 1/n_f²)