ভেক্টর বিনিময় সূত্র

ভেক্টর বিনিময় সূত্র একটা বিশেষ অবস্থা। সাধারণ অর্থে বিনিময় সূত্র বলতে বোঝায় 1 + 2 করলে যা হবে 2 + 1 করলে ঠিক তাই হবে, অর্থাৎ-

x + y = y + x

কাজেই A এবং B যদি দুটি ভেক্টর হয়, তবে তাদের জন্য বিনিময় সূত্রটি হবে-

A + B = B + A

এই বিনিময় সূত্রটি কোনো ভেক্টর রাশির জন্য সঠিক কিনা সেটা এখন আমরা যাচাই করে দেখবো।

প্রথমে আমরা দুটি ভেক্টর A এবং B কে আঁকি। ভেক্টরের ত্রিভুজ সূত্রানুসারে A এবং B ভেক্টরের লব্ধি হবে এদের দ্বারা কোনো ত্রিভুজের দুটি বাহু প্রকাশ করলে সেই ত্রিভুজের ৩য় বাহুর বিপরীত ক্রম বরাবর। অর্থাৎ XYZ ত্রিভুজের XY বরাবর A এবং YZ বরাবর B ভেক্টর ধরলে XZ বরাবর লব্ধি R = A + B পাওয়া যাবে। অর্থাৎ-

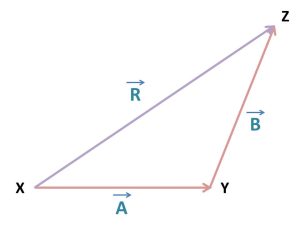
ছবি থেকে দেখো- XY + YZ = XZ

A + B = (A + B) …………(1)

এবার X বিন্দুতে B এর সমান করে একটা ভেক্টর আঁকি যার শীর্ষবিন্দু P. P থেকে A ভেক্টরের সমান করে আরেকটা PZ আঁকি যার শেষ বিন্দু Z.

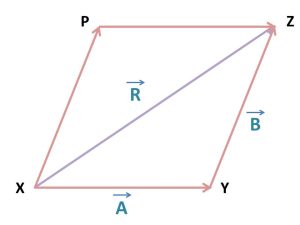
এখন নতুন তৈরি হওয়া ত্রিভুজটার দিকে লক্ষ্য করো, এই ত্রিভুজ থেকেও ভেক্টরের ত্রিভুজ সূত্র অনুসারে লেখা যায়-
XP + PZ = XZ
or, B + A = (A + B) …………(2)
(1) এবং (2) থেকে বোঝা যায়, ভেক্টর বিনিময় সূত্র মেনে চলে।