ভেক্টর বন্টন সূত্র

ভেক্টর বন্টন সূত্র বলতে বোঝায় দুটি ভেক্টরকে একটা স্কেলার রাশি দিয়ে গুণ করে তাদেরকে যোগ করলে যা মান পাওয়া যায়, সেই ভেক্টরের লব্ধিকে সেই একই স্কেলার রাশি দিয়ে গুন করলে ঠিক একই মান পাওয়া যায়।

যদি A এবং B দুটি ভেক্টর হয় এবং m যদি একটি স্কেলার রাশি হয় তবে বন্টন সূত্র অনুসারে-

m.A + m.B = m. (A+B)

ভেক্টরের ক্ষেত্রে এই ভেক্টর বন্টন সূত্রকে প্রমাণ করার জন্য এবার আমরা দুটি ভেক্টর A এবং B এর লব্ধি বের করবো। যদি A = OP এবং B = PQ হয়, তবে A ও B ভেক্টরের লব্ধি ভেক্টরের ত্রিভুজ সূত্র অনুসারে হবে-

OQ = OP + PQ

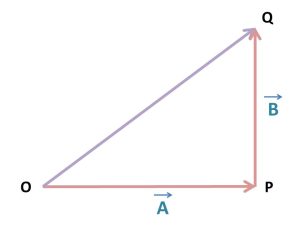
এবার A এবং B এই দুটো ভেক্টরকে m গুন বর্ধিত করলে আমাদের ভেক্টরের অবস্থা হবে ঠিক এমন-

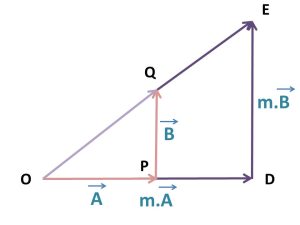
যেখানে OD = m.A এবং DE = m.B

এবার আমরা যদি OQ কে E পর্যন্ত বাড়াই তবে OE হবে আমাদের নতুন তৈরি কৃত ত্রিভুজের লব্ধি অর্থাৎ-

OE = OD + DE

এবার খেয়াল করো, আমাদের এখানে মোট দুইটা ত্রিভুজ রয়েছে, ত্রিভুজ POQ এবং ত্রিভুজ DOE. যেহেতু এদের প্রতিটা কোণ একে অপরের সমান, সেজন্য আমরা বলতে পারি এই ত্রিভুজ দুইটি সদৃশকোণী ত্রিভুজ। সদৃশকোণী ত্রিভুজের প্রতিটি বাহুর অনুপাত সমান থাকে, তাই এই দুটো ত্রিভুজ থেকে আমরা পাব-

OQ/OE = PQ/DE = OP/OD

আবার এই অনুপাতগুলো সবার মান হচ্ছে constant বা একই, যেটির মান m. তাহলে-

OE/OQ = DE/PQ = OD/OP = m

এবার আমরা দুটো ত্রিভুজের লব্ধি নিয়ে চিন্তা করি, লব্ধির অনুপাত-

OE/OQ = m

or, OE = m. OQ

আগেই আমরা OE এবং OQ এর মান বের করে ফেলেছি। তাই-

OE = m. OQ

or, OD + DE = m. (OP + PQ)

or, m. A + m. B = m (A + B)

তাহলে দেখা যাচ্ছে যে, এই ভেক্টর রাশি দুটো বন্টন সূত্র মেনে চলে। তাই এভাবে আমরা ভেক্টর বন্টন সূত্র প্রমাণ করতে পারি।