ভেক্টর যোগের সামান্তরিক সূত্র

ভেক্টর যোগের সামান্তরিক সূত্র বোঝার আগে আমরা একটা খেলার জিনিস নিয়ে কথা বলি, সেটা হচ্ছে গুলতি! তোমরা খেয়াল করে দেখবে, গুলতির মধ্যে একটা রাবারের ব্যান্ড লাগানো থাকে এবং রাবারের ব্যান্ড এর দুই প্রান্ত Y আকৃতির কোনো কাঠের দুই প্রান্তে লাগানো থাকে। যখন আমরা কোনো ইট বা পাথরকে এই রাবারের ব্যান্ড এর মাঝখানে রেখে টেনে ধরি তখন এই রাবারের ব্যান্ড নিজেদের দিকে গুলতির পাথরকে টেনে আনতে চায়। কিন্তু পাথরটি সবসময়ই রাবারের ব্যান্ড এর মাঝের অবস্থানে থেকে কাজ করে এবং মাঝ বরাবর সামনের দিকে ছুটে যায়। অর্থাৎ তোমরা নিচের ছবিটি যদি লক্ষ্য করো তাহলে বুঝতে পারবে রাবারের ব্যান্ড যে দুদিক বরাবর পাথরের উপর একটা বল দিচ্ছে সেই বল অনুযায়ী পাথরটি না গিয়ে বল দুটোর মাঝামাঝি জায়গা দিয়ে ছুটে যাবে-

তারমানে পাথরের উপর রাবারের ব্যান্ড যে দুটি বল প্রয়োগ করলো সেই বলের লব্ধি পাথরের উপর কাজ করে এবং পাথরটিকে মাঝখান বরাবর ছুড়ে মারে। এবার একটু খেয়াল করলে দেখতে পাবে, যদি রাবারের ব্যান্ড এর দুটি বলকে একটা সামান্তরিকের দুটি বাহু হিসেবে ধরে নেই তবে সেই সামান্তরিকের কর্ণ বরাবর রাবারের ব্যান্ড এর বল দুটোর লব্ধি কাজ করবে-

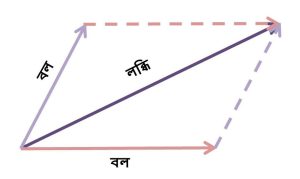
কাজেই আমরা বলতে পারি, যদি দুটি সমজাতীয় ভেক্টর একই সময় একটা সামান্তরিকের দুটি বাহু বরাবর কাজ করে, তবে সামান্তরিকের কর্ণটি দ্বারা সেই ভেক্টরের লব্ধি প্রকাশ পাবে। এটিকে ভেক্টর যোগের সামান্তরিক সূত্র।

দুটি ভেক্টরের লব্ধির মান

ধরা যাক দুটি সমজাতীয় ভেক্টর P এবং Q কে কোনো একটা সামান্তরিকের দুটি বাহু OA এবং OB দ্বারা প্রকাশ করলাম। তারমানে O বিন্দুতে P এবং Q সমজাতীয় ভেক্টর দুটি একই সময় কাজ করছে। এবার OB এর সমান্তরাল করে AC এবং OA এর সমান্তরাল করে BC আঁকি। তাহলে আমরা OACB একটি সামান্তরিক পাব। আমাদের জানা আছে, দুটি ভেক্টরের লব্ধি সামান্তরিকের কর্ণ বরাবর কাজ করে। তাহলে আমাদের এই সামান্তরিকের কর্ণ OC বরাবর কাজ করবে P এবং Q ভেক্টরের লব্ধি R. আর যেহেতু OB এবং AC সমান্তরাল, তাই OA এবং BC এরা দুজনও সমান্তরাল। আবার ধরা যাক P এবং Q ভেক্টর দুটি পরস্পর α কোণে কাজ করছে এবং P ভেক্টর এবং লব্ধি R ভেক্টর θ কোণে কাজ করছে-

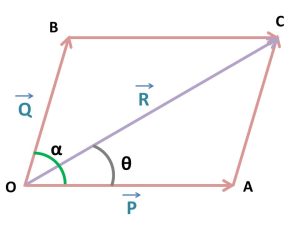
তাহলে আমরা বলতে পারি-

∠BOA = a

আমাদের কাজ হচ্ছে লব্ধি R এর মান বের করা। এর জন্য প্রথমে আমরা C বিন্দু থেকে একটি লম্ব CD আঁকি যেটি OA এর বর্ধিতাংশ কে D বিন্দুতে ছেদ করে। যেহেতু OCD একটি সমকোণী ত্রিভুজ তাই পিথাগোরাসের সূত্র মতে আমরা লব্ধি A অথবা OC এর মান পাব-

OC = √ (OD^2 + DC^2)

     or, R = √ (OD^2 + DC^2)

এখান থেকে আমাদের OD এবং DC এস এর মান জানা লাগবে। তবেই আমরা লব্ধি OC = R এর মান পাবো। CD এর মান জানার জন্য আমাদের CAD ত্রিভুজের দিকে লক্ষ করো, এটা একটি সমকোণী ত্রিভুজ।

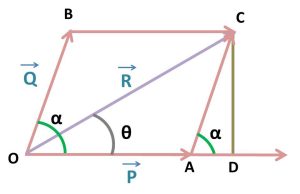
তাই CAD ত্রিভুজ থেকে-

∠DAC = α এবং cos α = AD / AC

or, AD = AC cos α

or, AD = Q cos α

এবার OD এর মান বের করার জন্য আমাদের ODC এই ত্রিভুজটি দেখতে হবে, যেটি একটি সমকোণী ত্রিভুজ। তাই এই ত্রিভুজ থেকে-

OD = OA + AD

আবার ত্রিভুজ ADC থেকে পেয়েছিলাম-

or, AD = Q cos α

তাই-

OD = OA + AD

or, OD = P + Q cos α

সবশেষে ত্রিভুজ ADC থেকে-

sin α = CD / AC

or, CD = AC sin α

or, CD = Q sin α

তাহলে লব্ধি R এর মান হবে-

R = √(OD^2 + DC^2)

or, R = √[(P + Q cos α)^2 + (Q sin α)^2]

or,  R = √ [P^2 + Q^2 + (sin^2α + cos^2α) + 2PQ cos α]

or, R = √ [ P^2 + 2PQ cos α + Q^2]

দুটি ভেক্টরের লব্ধির দিক

ভেক্টর P এর সাপেক্ষে লব্ধি R এর দিক হবে- θ

tanθ = Q sin α / (P + Q cos α)

θ = tan^-1 { Q sin α / (P + Q cos α) }

তাহলে এই সূত্র গুলো ভেক্টর যোগের সামান্তরিক সূত্র হিসেবে কাজ করবে।