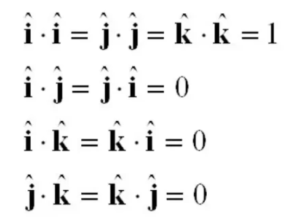স্কেলার গুণন

স্কেলার গুণন নিয়ে জানার আগে জানতে হবে ভেক্টর রাশির গুনন দুই ধরনের হতে পারে। যেমন-

• ভেক্টর রাশিকে স্কেলার রাশি দিয়ে গুন করা যায়
• ভেক্টর রাশিকে ভেক্টর রাশি দিয়ে গুন করা যায়।

ভেক্টর রাশিকে স্কেলার রাশি দিয়ে গুন

যেকোনো ভেক্টর রাশিকে তুমি যদি কোনো স্কেলার রাশি দিয়ে গুন করো তবে সেই গুনফল একটা ভেক্টর রাশি হয়।

যেমন A একটা ভেক্টর রাশি, m একটা স্কেলার রাশি। এদেরকে গুন করলে নতুন একটা গুনফল পাওয়া যাবে- mA এবং এর মান হবে = |mA|

আবার m এর মান যদি -ve হয় তবে mA ভেক্টরের দিক হবে A এর বিপরীত দিকে। এই ধরনের গুননের ছোট্ট একটা বাস্তব উদাহরণ দেখি-
কোনো বস্তুর ভর m একটা স্কেলার রাশি এবং ত্বরন a একটি ভেক্টর রাশি। আর এদের গুনফল F = ma এটিও একটি ভেক্টর রাশি। আর F এর দিক হচ্ছে a এর দিক বরাবর।

 

ভেক্টর রাশিকে ভেক্টর রাশি দ্বারা গুন

দুটো ভেক্টর রাশিকে যখন গুন করা হয় তখন দুটো ঘটনা ঘটতে পারে। এদের গুনফল স্কেলারও হতে পারে আবার ভেক্টরও হতে পারে।

• দুটো ভেক্টর রাশিকে “ডট গুন” বা “স্কেলার গুন” করা হলে গুনফল হবে স্কেলার রাশি।
• আবার দুটো ভেক্টর রাশিকে “ক্রস গুনন” বা “ভেক্টর গুন” করলে সেই গুনফল হবে ভেক্টর রাশি।

স্কেলার গুণন (ডট গুণন)

দুটি ভেক্টর রাশির স্কেলার গুণফল একটি স্কেলার রাশি হবে যার মান রাশি দুটির মান এবং তাদের মধ্যবর্তী কোণের কোসাইনের (cosine) গুণফলের সমান। অর্থাৎ স্কেলার গুন cosine এর সূত্র মেনে চলে। অন্যভাবে বললে দুটি ভেক্টর রাশির যে গুণনের ফলে একটি স্কেলার রাশি পাওয়া যায় তাকে ভেক্টরদ্বয়ের স্কেলার গুণফল বলে। বা, দুটি ভেক্টরের মানের গুণফলের সাথে তাদের মধ্যবর্তী কোণের কোসাইনের গুণফলকে স্কেলার গুণফল বা ডট গুণফল বলে।

ভেক্টর রাশি দুটির মাঝে (.) চিহ্ন দিয়ে ডট গুণফল প্রকাশ করা হয় এবং পড়তে হয় “প্রথম রাশি ডট দ্বিতীয় রাশি।”

মনে করো A, B দুটি ভেক্টর রাশি। এরা পরস্পরের সাথে α কোণে আনত। তাদের স্কেলার বা ডট গুণফল = A.B, যাকে পড়ার সিস্টেম ভেক্টর A ডট ভেক্টর B।

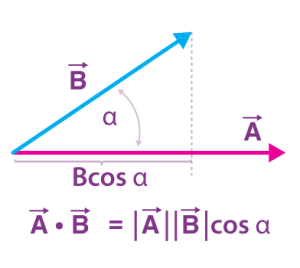
কাজেই সংজ্ঞা অনুসারে পাই,

A.B =|A||B|cosα

or, A.B = A(Bcosα)

এখানে Bcosα হচ্ছে A এর দিকে B এর উপাংশের মান বা A এর উপর B এর লম্ব অভিক্ষেপ।

আবার, A.B = BAcosα

or, A.B = B(Acosα)

কিন্তু এবার Acosα হচ্ছে B এর দিকে A এর উপাংশের মান বা B এর A এর লম্ব অভিক্ষেপ।

সুতরাং যে কোনো দুটি ভেক্টরের বেলার গুণফল বলতে যে কোনো একটি ভেক্টরের মান এবং সেই ভেক্টরের দিকে অপর ভেক্টরের উপাংশের বা সেই ভেক্টরের উপর অপর ভেক্টরের লম্ব অভিক্ষেপের গুণফলকে বুঝায়।

বিশেষ দ্রষ্টব্য

• যদি α = 0º হয়, তবে A.B = ABcos0 = AB, এক্ষেত্রে ভেক্টর দুটি পরস্পরের সমান্তরাল হবে।
• যদি α = 90º হয়, তবে A.B = ABcos90 =, 0 এক্ষেত্রে ভেক্টর দুটি পরস্পর লম্ব হবে।
• যদি α = 180º deg হয়, তবে A.B = ABcos180 = -AB আসবে।  এক্ষেত্রে ভেক্টর দুটি পরস্পরের সমান্তরাল এবং বিপরীতমুখী হবে।

স্কেলার গুণনের উদাহরণ

বল F এবং সরণ s উভয়েই ভেক্টর রাশি। কিন্তু এদের স্কেলার গুণফল কাজ (W) একটি স্কেলার রাশি, অর্থাৎ

W= F.s = Fs cosα

এছাড়া স্থিতিশক্তি, বৈদ্যুতিক বিভব ইত্যাদিও ভেক্টর রাশির স্কেলার গুণফলের উদাহরণ।

একক ভেক্টর রাশির স্কেলার গুণন

পরস্পর সমকোণে অবস্থিত তিনটি অক্ষ বিবেচনা করি। এরা যথাক্রমে X, Y এবং Z। এই তিনটি অক্ষ বরাবর প্রকাশ বরলে তিনটি একক ভেক্টর হবে যথাক্রমে i, j, k। এদের স্কেলার গুণফল গুলো হবে-