স্কেলার রাশি ও ভেক্টর রাশি

ভৌতজগতে যা কিছু পরিমাপ করা যায় তাকেই রাশি বলে। যেমন – কোনো বস্তুর দৈর্ঘ্য, ভর, আয়তন, ঘনত্ব ইত্যাদি পরিমাপ করা যায়। এগুলো সবই রাশি। কোনো রাশি যখন পরিমাপ করা হয় তখন তার একটি মান থাকে। এই মান প্রকাশ করতে আমরা একটি সংখ্যা এবং একটি একক ব্যবহার করি। যেমন, আমরা যদি বলি রনির উচ্চতা 1.5 মিটার, তাহলে বুঝা যায় দৈর্ঘ্যের একক মিটার, আর রনির উচ্চতা তার 1.5 গুণ। কিন্তু কেবল মান দিয়েই সকল রাশিকে সম্পূর্ণরূপে প্রকাশ করা যায় না। যেমন, আমরা যদি বলি একটি গাড়ি ঘন্টায় 30 কিলোমিটার বেগে চলছে, তাহলে এটা বুঝা যাবে যে গাড়িটি এক ঘন্টায় 30 কিলোমিটার দূরত্ব অতিক্রম করেছে, কিন্তু গাড়িটি কোন দিকে সেই দূরত্ব অতিক্রম করেছে তা জানা যাবে না। গাড়িটির প্রকৃত অবস্থা বুঝতে হলে গাড়িটির বেগ কোন দিকে সেটাও উল্লেখ করতে হবে। দিকের বিবেচনায় আমরা বস্তুজগতের সকল রাশিকে দুই ভাগে ভাগ করতে পারি- স্কেলার রাশি ও ভেক্টর রাশি।

স্কেলার রাশি

যে সকল ভৌত রাশিকে শুধু মান দ্বারা সম্পূর্ণরূপে প্রকাশ করা যায়, দিক নির্দেশের প্রয়োজন হয় না তাদেরকে স্কেলার রাশি বলে। দৈর্ঘ্য, ভর, দ্রুতি,কাজ,শক্তি,সময়,তাপমাত্রা ইত্যাদি স্কেলার রাশির উদাহরণ। এদের শুধুমাত্র মান থাকে, যেমন- 5kg ভর, 3m দুরত্ব।

ভেক্টর রাশি

যে সকল ভৌত রাশিকে সম্পূর্ণরূপে প্রকাশ করার জন্য মান ও দিক উভয়ের প্রয়োজন হয় তাদেরকে ভেক্টর রাশি বলে। যদি কোনো রাশির শুধুমাত্র মান থাকে তবে সেটি ভেক্টর রাশি হতে পারবে না। ঠিক তেমনিভাবে যদি কোনো রাশির শুধুমাত্র দিক থাকে তবে সেটিও ভেক্টর রাশি হতে পারবে না। ভেক্টর রাশির কিছু উদাহরণ হল- সরণ, ওজন, বেগ,ত্বরণ, বল, তড়িৎ তীব্রতা, চৌম্বক তীব্রতা ইত্যাদি।

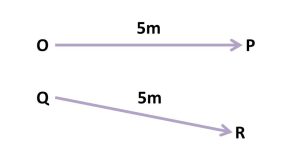
খেয়াল করো, একটা রেখা OP কে, যেটি একটি ভেক্টর নির্দেশ করছে। কারণ এর মান ধরা যাক 5 মিটার এবং এর দিক ধরা যাক ডান দিকে। একইভাবে QR কে দেখো, এটিও একটি ভেক্টর রাশি। কারণ এটির মান ধরা যাক 5 মিটার এবং এটির দিক ধরা যাক বাম দিকে। যদিও ভেক্টর দুটোর মান সমান কিন্তু এরা দুজন কখনোই সমান ভেক্টর হবে না, কেননা এদের দিক পরস্পর বিপরীতমুখী। তাহলে বোঝা গেল, দুটো ভেক্টর তখনি সমান হবে যখন তাদের মান এবং দিক দুটোই সমান হবে।

নিচের সারণি থেকে দেখা যাচ্ছে যে, প্রতিটি ভেক্টরকে মান ও দিক দিয়ে আর স্কেলার রাশিগুলোকে কেবল মান দিয়ে নির্দেশ করা হয়েছে-

স্কেলার রাশি

ভেক্টর রাশি

নাম	সংকেত	উদাহরণ	নাম	সংকেত	উদাহরণ
দুরত্ব	d	40 m	সরণ	S	40 m পূর্ব দিকে
দ্রুতি	v	30 ms-1	বেগ	v	30 ms-1উত্তর দিকে
সময়	t	15 s	বল	F	100 N উপরের দিকে
শক্তি	E	2000 J	ত্বরণ	a	98 ms-2 নিচের দিকে

ভেক্টর রাশির প্রকাশ

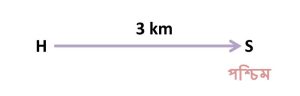
ধরো তুমি তোমার বাসা থেকে পশ্চিম দিকে নির্দিষ্ট দূরত্বে 3 কিলোমিটার দূরে তোমার স্কুলে হেঁটে গেলে। এখানে তোমার বাসা হচ্ছে তোমার যাত্রার আদি বিন্দু এবং স্কুল হচ্ছে শেষ বিন্দু। তাহলে বাসা থেকে স্কুলের যে দূরত্ব সেটা একটা মান (3 km) এবং তোমার স্কুল বাসা থেকে যেদিকে অবস্থান করছে সেদিকটা হচ্ছে একটা direction বা দিক (পশ্চিম দিক)। তোমার বাসাকে যদি H বিন্দু এবং স্কুলকে যদি S বিন্দু দিয়ে প্রকাশ করি তবে তোমার যাত্রাপথের ভেক্টর হবে H এবং S এর মধ্যকার দুরত্ব এবং দিক দুটো মিলিয়ে। যেকোনো ভেক্টর রাশি প্রকাশ করার জন্য তার মাথায় একটা তীর দেওয়া হয়। আবার কিছু কিছু সময় ভেক্টর রাশি প্রকাশের জন্য বিভিন্ন প্রতীক ব্যবহার করা হয়। তাই তোমার বাসা থেকে স্কুলে যাওয়ার ভেক্টরকে প্রকাশ করা হয় ঠিক এভাবে- →HS এভাবেই ভেক্টর রাশিকে প্রকাশ করা হয়।

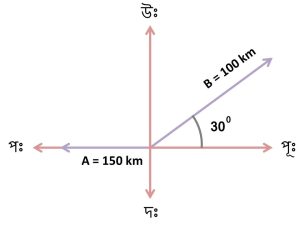
আবার নিচের চিত্রে দেখো, ভেক্টর রাশিকে একটি তীর চিহ্নিত সরলরেখা দ্বারা নির্দেশ করা হচ্ছে। A ও B দুটি সরলরেখার দৈর্ঘ্য ভেক্টর রাশিটির মান এবং তীর চিহ্ন এর দিক নির্দেশ করছে। উদাহরণ স্বরূপ এই চিত্রে A দ্বারা 150 km সরণকে নির্দেশ করা হয়েছে। সুতরাং এই চিত্রে A ভেক্টরটি পশ্চিম দিকে 150 km সরণ নির্দেশ করছে। আবার B ভেক্টরটি পূর্বদিকের সাথে 30 কোণে উত্তর দিকে 100 km সরণ নির্দেশ করছে।

ভেক্টর রাশির নির্দেশনা

কোন রাশির সংকেতের উপর তীর চিহ্ন দিয়ে ভেক্টর রাশি নির্দেশ করা হয়, যেমন A→। A বা। A→। ভেক্টর রাশি A→ এর মান নির্দেশ করে। ছাপার ক্ষেত্রে অনেক সময় A→এর পরিবর্তে বোল্ড হরফ A দিয়ে ভেক্টর এবং সাধারণ হরফ A দিয়ে রাশিটির মান প্রকাশ করা হয়। দুই বা ততোধিক এক জাতীয় ভেক্টর রাশি যোগ করলে একটি নতুন ভেক্টর রাশি পাওয়া যায়। এ নতুন রাশিটিকে দুই বা ততোধিক ভেক্টর রাশির লব্ধি বলে। আর যে ভেক্টরগুলো যোগ করে লব্ধি ভেক্টর পাওয়া যায় তাদের প্রত্যেককে লব্ধি ভেক্টরের উপাংশ বলে। যোগের জন্য ভেক্টর রাশি দুইটি অবশ্যই একই জাতীয় হতে হবে। বেগ, ত্বরণ ইত্যাদি ভেক্টর রাশি। বেগের সাথে বেগ কিংবা ত্বরণের সাথে ত্বরণের যোগ সম্ভব। কিন্তু বেগের সাথে ত্বরণের যোগ সম্ভব নয়। এ কথাটি অবশ্য স্কেলার রাশির ক্ষেত্রেও প্রযোজ্য। যেমন – তাপমাত্রার সাথে শক্তির যোগ সম্ভব নয়।