শ্রোডিঙ্গার সমীকরণ

বোর পরমাণু মডেল, হাইজেনবার্গের অনিশ্চয়তা নীতি, ডি-ব্রগলির ইলেকট্রনের কণাধর্ম ও তরঙ্গ ধর্মের দ্বিত্ব প্রকৃতির সম্পর্ক এবং ইলেকট্রনের স্থির শক্তিস্তরের ধারণা দ্বারা বর্ণালীর ব্যাখ্যা নিখুঁতভাবে দিতে পারে না। এ তিনটি বিষয়কে গণ্য করে ১৯২৬ খ্রিস্টাব্দে শ্রোডিঙ্গার পরমাণুর তরঙ্গ বলবিদ্যা মডেল প্রস্তাব করেন। এ মডেলে শ্রোডিঙ্গার ইলেকট্রনকে তরঙ্গ ও কণা উভয় বা দ্বিত্ব প্রকৃতিযুক্ত প্রস্তাব করেন। এ তরঙ্গরূপী ইলেকট্রনসমূহ ধনাত্মক চার্জযুক্ত নিউক্লিয়াসের চারদিকে ত্রিমাত্রিকভাবে ঘূর্ণায়মান থাকে। তরঙ্গরূপী ইলেকট্রনের সুষ্ঠুভাবে ব্যাখ্যার জন্য শ্রোডিঙ্গার একটি ত্রিমাত্রিক (x, y, z) তরঙ্গ গতীয় সমীকরণ উপস্থাপন করেন, যা শ্রোডিঙ্গার সমীকরণ নামে পরিচিত।

E = ইলেকট্রনের মোট শক্তি, u = ইলেকট্রনের স্থিতিশক্তি, h = প্ল্যাংকের ধ্রুবক, Ψ = x, y, z অক্ষ বরাবর সমকোণেস্থিত অক্ষ।

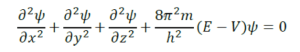
Ψ ও Ψ² এর বৈশিষ্ট্য

• শ্রোডিঙ্গারের দ্বিতীয় অন্তরক সমীকরণ (second order differential equation) সমাধান করে E এর যে সব অর্থবহ নির্দিষ্ট মান পাওয়া যায়, এদেরকে আইজেন মান (Eigen values) বলা হয়। এ সব মান দ্বারা পরমাণুতে কতকগুলো নির্দিষ্ট শক্তিস্তর বা অরবিটকে বুঝায়।
• পরমাণুর বেলায় E এর প্রত্যেকটি মানের সাথে সংশ্লিষ্ট Ψ এরও কতকগুলো বিশেষ মান আছে। তখন ঐ বিশেষ মানযুক্ত তরঙ্গ ফাংশন Ψ কে আইজেন ফাংশন (Eigen function) বলা হয় এবং E এর মানগুলোকে আইজেন মান বলা হয়।
• Ψ এর কোন ভৌত তাৎপর্য নেই। এটি শুধু ইলেকট্রনের তরঙ্গের বিস্তৃতি (amplitude) প্রকাশ করে।
• Ψ² এর মান বিশেষ অর্থ প্রকাশ করে। Ψ² এর প্রতিটি মান ইলেকট্রনের তরঙ্গের তীব্রতার সমানুপাতিক। কোন নির্দিষ্ট শক্তির ইলেকট্রনের সম্ভাব্য অবস্থান নিউক্লিয়াসের চারদিকে কোন স্থানে হবে তা Ψ² এর মান থেকে জানা যায়।
• নিউক্লিয়াসের চারদিকে যে নির্দিষ্ট ত্রিমাত্রিক স্থানে কোন নির্দিষ্ট শক্তির ইলেকট্রনের অবস্থানের সম্ভাবনা বেশি যেমন প্রায় 90-95% হয়, একে বিজ্ঞানী সমারফিল্ড অরবিটাল (orbnal) নামে অভিহিত করেন। সুতরাং Ψ² এর মানসমূহ পরমাণুতে বিভিন্ন শক্তির অরবিটাল প্রকাশ করে। 
• প্রকৃতপক্ষে পরমাণুতে বিভিন্ন অরবিট বা শক্তিস্তরে ইলেকট্রনের বিভিন্ন উপশক্তিস্তর ও অরবিটাল আছে, তা পূর্ণাঙ্গ ব্যাখ্যার জন্য চার প্রকারের পরস্পর সম্পর্কযুক্ত সংখ্যামান প্রস্তাব করা হয়, এদেরকে কোয়ান্টাম সংখ্যা বলা হয়। তাই বলা যায়, শ্রোডিঙ্গার সমীকরণ ব্যবহার করে কোয়ান্টাম সংখ্যা তৈরি করা হয়েছে।

পরমাণুতে ইলেকট্রনের অবস্থান

আমরা পরমাণুর বিভিন্ন মডেল থেকে এটা জানতে পারি যে পরমাণুর ঠিক কেন্দ্রে নিউক্লিয়াস নামক একটা জায়গা থাকে এবং এই নিউক্লিয়াসকে ঘিরে চারপাশে বৃত্তাকার পথে ইলেকট্রন ঘুরতে থাকে। কিন্তু এই কথাটা পুরোপুরি সত্য না। কারণ পরমাণুতে ইলেকট্রন কখনোই সুষম বৃত্তাকার পথে আবর্তন করে না, একটা নির্দিষ্ট সীমা বা জায়গার মধ্যে এটি আবর্তন করে।

তবে এখানেও একটা কথা আছে। ইলেকট্রন পরমাণুর নিউক্লিয়াসের বাইরে ঠিক কোন বিন্দুতে আছে সেটা আবার কখনোই বের করা সম্ভব হয় না। যেকোনো বিন্দুর কেবল একটা সম্ভাব্যতা বের করা যায় যে সেখানে ইলেকট্রন থাকার সম্ভাবনা কতটুকু।

নিউক্লিয়াসের চারপাশের জায়গাটা ত্রিমাত্রিক বা 3D, তাই আমরা একটা ত্রিমাত্রিক স্থানাংক ব্যবস্থার সাহায্য নিবো ইলেকট্রনের অবস্থান বের করার জন্য। ধরা যাক নিউক্লিয়াসটি হচ্ছে আমাদের মূল বিন্দু। এখন নিউক্লিয়াসের বাইরে P অবস্থানে ইলেকট্রন আছে কি নাই সেটার সম্ভাবনা আমরা বের করবো। তাহলে ত্রিমাত্রিক স্থানাংক ব্যবস্থায় P বিন্দুর স্থানাংক হবে = (x, y, z)।

আবার যদি পোলার কার্তেসীয় স্থানাংকের সাহায্য নেই তবে নিউক্লিয়াস বা মূলবিন্দু থেকে r দুরত্বে, ভূমি বরাবর φ কোণে এবং লম্ব বরাবর θ কোণে P বিন্দুর স্থানাংক পাওয়া যাবে যার মান P (r, θ, φ)।

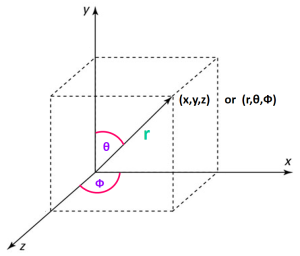
যেহেতু নিউক্লিয়াসের চারপাশে ইলেকট্রন সুষম বৃত্তাকার পথে চলাচল করে না তাই আমাদের এমন একটা ফাংশন বের করতে হবে যেখানে নিউক্লিয়াসকে মূলবিন্দু (0, 0, 0) ধরে কোনো বিন্দুর মান (x, y, z) বা (r, θ, φ) বসালে আমরা সেই ফাংশনের মাধ্যমে জেনে যাবো P বিন্দুতে ইলেকট্রন থাকার সম্ভাবনা কতটুকু।

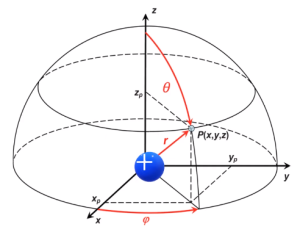
তবে মজার ব্যাপার হচ্ছে, বিজ্ঞানী স্রোডিঞ্জার সেই ফাংশটিকে বা সমীকরণটিকে বের করে রেখেছিলেন। এটিকে স্রোডিঞ্জারের সমীকরণ বলে। একটা পরমাণুতে একটা নির্দিষ্ট স্থানে ইলেকট্রন পাওয়ার সম্ভাবনা বের করার জন্য স্রোডিঞ্জারের সমীকরণ ব্যবহার করা হয়।

আমরা উপরের সমীকরণ বা ফাংশনকে সাই (Ψ) ব্যবহার করে ভেঙ্গে লিখতে পারি-

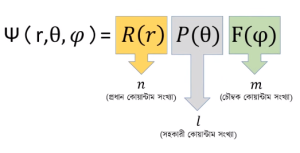
   Ψ (r, θ, φ) = R (r) P (θ) F (φ)

কাজেই নিউক্লিয়াসের বাইরের যেকোনো একটা বিন্দুর Ψ (r, θ, φ) কে যদি আমরা উপরের ফাংশনে বসাই তবে স্রোডিঞ্জারের সমীকরণের মাধ্যমে সেই বিন্দুতে ইলেকট্রন থাকার সম্ভাবনা পেয়ে যাবো।

এখন, ফাংশনের R (r), P (θ) এবং F (φ) কে যথাক্রমে প্রধান কোয়ান্টাম সংখ্যা, সহকারী কোয়ান্টাম সংখ্যা এবং চৌম্বক কোয়ান্টাম সংখ্যা বলে। তবে Ψ এর আলাদা কোনো কাজ না থাকলেও Ψ² এর কাজ আছে। যদি এই তিনটির মান বসানোর পর Ψ² এর মান 25 আসে, তবে বুঝতে হবে সেই অবস্থানে ইলেকট্রন থাকার সম্ভাবনা 25%।