ধাতুসমূহের কেলাসে শুধুমাত্র ধাতব বন্ধন বিদ্যমান, কিন্তু ধাতুসমূহের গঠন বিভিন্ন ধরনের হয়। তবে অধিকাংশ ধাতু তিনটি প্রধান ধরনের গঠনের মধ্য থেকে যেকোন এক ধরনের কেলাসের মাধ্যমে গঠিত। যেহেতু একই ধাতুর কেলাসে সব পরমাণু একই ধরনের এবং একই সাইজের, সেহেতু ধাতু কেলাস গঠনের সময় সর্বনিম্ন স্থিতিশক্তি অর্জনের জন্য পরমাণুসমূহ যতদূর সম্ভব পরস্পরের কাছাকাছি অবস্থান করবে এবং প্রতিটি পরমাণু যত বেশি সংখ্যক পরমাণু দ্বারা পরিবেষ্টিত হবে, পরমাণুসমূহকে গোলকাকৃতি হিসেবে গণ্য করা যাবে।
নিচের ছবিতে দেখো, সমান গোলকসমূহের একটি স্তরে সম্ভাব্য সবচেয়ে ঘন সন্নিবেশ অবস্থা দেখানো হয়েছে। এবার একটি পরমাণুর নাম ধরি A। খেয়াল করে দেখো, A এর চারদিকে ছয়টি গোলক বা পরমাণু এই পরমাণুকে স্পর্শ করে অবস্থান করতে পারে। ৬টা গোলকের কেন্দ্রকে যোগ করলে একটি নিয়মিত ষড়ভুজ পাওয়া যায়। অপরদিকে পরস্পরবিরোধী স্পর্শকারী তিনটা গোলককে এক একটি গ্রুপ হিসেবে ধরা যায়। এ তিনটি গোলকের মধ্যবিন্দু যোগ করলে একটি সমবাহু ত্রিভুজ পাওয়া যায়। এ তিনটি গোলকের মাঝখানে কিছু ফাঁকা জায়গা থাকে। যদি একটি স্তরে পরস্পর স্পর্শকারী কিছু গোলক রেখে তার উপর আরেকটি গোলক রাখা হয়, তবে তা তিনটি গোলকের মাঝখানে ফাঁকা জায়গার উপরের স্থান দখল করবে, এর পরেও এ চারটি গোলকের মাঝখানে ফাঁকা জায়গা থেকে যায়। এ চারটি গোলকের মাঝখানের ফাঁকা জায়গাকে চতুস্তলকীয় ছিদ্র বা স্থান (tetrahedral bole or site) বলা হয়। কেননা এ স্থান এমন চারটি গোলক দ্বারা পরিবেষ্টিত, যাদের কেন্দ্র একটি সুষম চতুস্তলকের শীর্ষবিন্দুসমূহে অবস্থান করে। কেলাস গঠন বোঝার জন্য এ ছিদ্র খুবই গুরুত্বপূর্ণ।
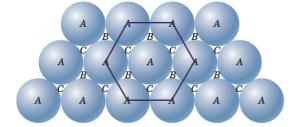
যদি একটি স্তরে বেশ কিছু গোলক রেখে তার উপরে বেশ কিছু সংখ্যক গোলক রাখা হয়, তবে এ গোলকসমূহ প্রথম স্তরের ছিদ্র বা ফাঁকা জায়গাসমূহে (hole or site) এ অবস্থান নেবে, এর ফলে প্রথম স্তরের উপর আরেকটি স্তরের সৃষ্টি হয়।
এখন প্রথম স্তরের ঠিক নিচে তৃতীয় আরেকটি স্তরের কথা চিন্তা করা যায়। এ স্তরটি দ্বিতীয় স্তরের অনুরূপ, শুধু অবস্থান ভিন্ন। সুতরাং এ স্তরের ৪টি গোলক প্রথম স্তরের কেন্দ্রীয় গোলকের সংস্পর্শে আসবে। সুতরাং প্রথম স্তরের কেন্দ্রীয় গোলকের সংস্পর্শে সর্বমোট ১২টি গোলক অবস্থান করবে, তন্মধ্যে ছয়টি একই স্তরের তিনটি ঠিক উপরের স্তরের এবং বাকি তিনটি ঠিক নিচের স্তরের। সুতরাং এর সন্নিবেশ সংখ্যা ১২। সমান ব্যাসার্ধ বিশিষ্ট গোলকসমূহের ক্ষেত্রে ১২ই হচ্ছে সম্ভাব্য সর্বোচ্চ সন্নিবেশ সংখ্যা এবং সবচেয়ে ঘন সন্নিবেশিত অবস্থা। সব ধাতুর ক্ষেত্রে এ সন্নিবেশ সংখ্যা দেখা যায়।
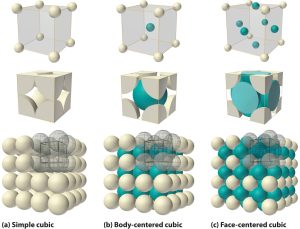
কঠিন অবস্থার রসায়নে ত্রিমাত্রিকভাবে একটি পরমাণুর সংস্পর্শে যতটি পরমাণু বিদ্যমান তাকে ঐ পরমাণু সংখ্যাকে সে পরমাণুর সন্নিবেশ সংখ্যা (co-ordination number, সংক্ষেপে CN) বলা হয়। এখন দুটি স্তরের উপর অবস্থানরত তৃতীয় স্তরের গোলকসমূহের দিকে একটু গভীরভাবে নজর দেয়া যাক।
এক্ষেত্রে দুটি ভিন্ন ধরনের বিন্যাস সম্ভব। মধ্যবর্তী স্তরের কেন্দ্রীয় গোলকের যে সব ফাঁকা জায়গা আছে, তাদেরকে যদি 1,2,1,2,1,2 দ্বারা চিহ্নিত করি, তবে এর উপরের নিচের স্তরে গোলক রাখা হলে যে গোলকগুলো হয় 1, 1, 1 বা 2, 2, 2 চিহ্নিত ফাঁকা জায়গায় অবস্থান নিতে পারে। দুটি স্তর বিবেচনা করলে 1, 1, 1 বা 2, 2, 2 অবস্থানের মধ্যে কোন পার্থক্য নেই, কিন্তু এটি সহ উপর নিচে মোট তিনটি স্তর বিবেচনা করলে পার্থক্য দেখা যায়।
