ভেক্টর অভিক্ষেপ ও উপাংশ এই দুটোকে একই রকম মনে হলেও এদের মাঝে খুব সামান্য পরিমান পার্থক্য আছে।
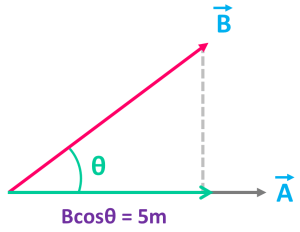
অভিক্ষেপ হচ্ছে একটা ভেক্টরের উপর আরেকটা ভেক্টরের ছায়া। যেমন নিচের ছবিতে দেখো A ভেক্টরের উপর B ভেক্টরের ছায়া পড়েছে যার মান – Bcost. কিন্তু অভিক্ষেপের কোনো দিক থাকে, শুধুমাত্র মান থাকে। যেমন ছায়াটার দৈর্ঘ্য এখানে 5m.
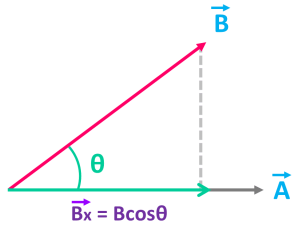
একটা ভেক্টরের একটা অংশ যদি অন্য ভেক্টর বরাবর নির্দিষ্ট দিকে কাজ করে তবে সেটাই হচ্ছে উপাংশ। যেমন নিচের ছবিতে দেখো, B ভেক্টরের অভিক্ষেপ A ভেক্টর বরাবর একটা নির্দিষ্ট দিকে কাজ করছে। তাই দিক সহ অভিক্ষেপের মানকে উপাংশ বলে। A ভেক্টরের উপর B ভেক্টরের উপাংশটি হবে Bx = Bcosθ
তাই তোমরা বলতে পারো,
অভিক্ষেপ = |উপাংশ|
অর্থাৎ অভিক্ষেপ হচ্ছে মান, আর এই মানের সাথে একটা দিক যুক্ত করে দিলে সেটাই উপাংশ হয়ে যাবে। অভিক্ষেপের সাথে কখনোই i, j, k ইত্যাদি একক ভেক্টর থাকেনা কিন্তু উপাংশের সাথে একক ভেক্টর হিসেবে এরা যুক্ত থাকে।
আবার যদি উপাংশ থেকে অভিক্ষেপ বের করতে চাই তবে সেটার সূত্র হবে-
উপাংশ = অভিক্ষেপ * একক ভেক্টর
এখানে যার উপর আমরা অভিক্ষেপ নিবো তার একক ভেক্টরটি হচ্ছে এটি। ব্যাপারটা ক্লিয়ার হবার জন্য একটা ছোট্ট উদাহরণ দেখি। নিচের ছবিটি দেখো-
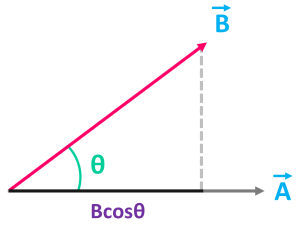
এখানে A এর উপর B এর অভিক্ষেপ = |B| cosθ
কিন্তু A এর উপর B এর উপাংশ হবে = (|B| cosθ) x (A এর একক ভেক্টর)
আবার নিচের ছবিটি দেখো-
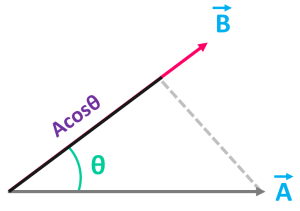
এখানে B এর উপর A এর অভিক্ষেপ = |A| cosθ
তাই B এর উপর A এর উপাংশ হবে = (|A| cosθ) x (B এর একক ভেক্টর)
তাই বলা যায়, ভেক্টর অভিক্ষেপ ও উপাংশ দুটো ভিন্ন জিনিস।
