ভেক্টর রাশি সম্পর্কিত সংজ্ঞা – ২

ভেক্টর রাশি সম্পর্কিত আরো অনেকগুলো সংজ্ঞা নিয়ে আমরা এখানে জানার চেষ্টা করবো।

 

সমতলীয় ভেক্টর (Co-planner Vector)

সমতলীয় অর্থ হচ্ছে যারা একই তল বরাবর থাকে। যে সকল ভেক্টর একই তল বরাবর থাকে তাদেরকে সমতলীয় ভেক্টর বলে।
ধরো তুমি এবং তোমার দুজন বন্ধু একটা ছাদের উপর দাঁড়িয়ে আছ। হঠাৎ তোমরা তিনজনই নির্দিষ্ট তিনটি দিকে হাঁটা শুরু করলে। এখানে তোমাদের তিনজনেরই সরণ হচ্ছে, যদিও তোমাদের দিক ভিন্ন। কাজেই তোমাদের তিনজনের সরণ ভেক্টরটি হচ্ছে সমতলীয় ভেক্টর।

মনে রাখতে হবে, সমতলীয় ভেক্টরের ক্ষেত্রে প্রতিটা ভেক্টরের মান এবং দিক একই হবার কোনো প্রয়োজন নেই।

 

বিপ্রতীপ ভেক্টর (Reciprocal Vector)

যদি দুটো ভেক্টরের দিক একই হয় এবং তারা যদি সমজাতীয় হয় তবে ভেক্টর দুটিকে বিপ্রতীপ ভেক্টর বলে। তবে বিপ্রতীপ ভেক্টরের একজনের মান অপরজনের মানের বিপরীত হয়। যেমন 5 এর বিপরীত মান 1/5.

যদি 𝑨⃗ = 5i হয়, তবে এর বিপরীত ভেক্টরের মান হবে-
𝑩⃗ = (1/5)i হবে

 

একক ভেক্টর (Unit Vector)

যেসব ভেক্টরের মান 1 তাদেরকে একক ভেক্টর বলে। কোনো ভেক্টরকে তার মান দিয়ে ভাগ করলে সেই ভেক্টরের একক ভেক্টর পাওয়া যায়। যদি কোনো  ভেক্টরের মান 𝑨⃗ = 3i – 4j + 5k হয়, তবে এর একক ভেক্টরের মান হবে-

𝑨⃗/|𝑨⃗| = 3i – 4j + 5k / 25

একক ভেক্টর কে প্রকাশ করা হয় একটা ছোট হাতের লেটার এবং এর উপরে একটা টুপি চিহ্ন বসিয়ে, যেমন : â =  3i – 4j + 5k / 25

 

আয়ত একক ভেক্টর (Rectangular Unit Vector)

আয়ত একক ভেক্টর নিয়ে জানার জন্য প্রথমে আমাদের জানতে হবে ত্রিমাত্রিক স্থানাংক ব্যবস্থা নিয়ে, যেখানে তিন দিক বরাবর তিনটা অক্ষ থাকে X, Y, Z থাকে। ধরা যাক O আমাদের মূল বিন্দু এবং O থেকে X, Y, Z এই তিন দিকে তিনটি অক্ষ বরাবর তিনটি রেখা চলে গিয়েছে। যদি এই ত্রিমাত্রিক ব্যবস্থায় একটা পয়েন্ট বা বিন্দু P হয়, তবে তার ত্রিমাত্রিক অবস্থান বা স্থানাংক হবে- P (x,y,z).

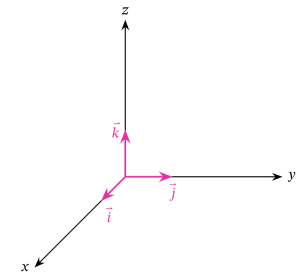
এবার আমরা ত্রিমাত্রিক স্থানাংক ব্যবস্থায় তিনটা অক্ষকে (X, Y, Z অক্ষ) ক্ষুদ্র ক্ষুদ্র ভাগে ভাগ করে নেই। X অক্ষ বরাবর প্রত্যেকটা ঘরকে বলা হয় i, Y অক্ষ বরাবর প্রত্যেকটা ঘরকে বলা হয় j এবং Z অক্ষ বরাবর প্রত্যেকটা ঘরকে বলা হয় k.এখানে i, j, k এরা তিনজন তিনটি অক্ষ বরাবর একক ভেক্টর হিসেবে কাজ করছে। তিনটি অক্ষ নিয়ে একক ভেক্টরের এই অবস্থানকে বলা হয় আয়ত একক ভেক্টর।

অবস্থান ভেক্টর (Position Vector)

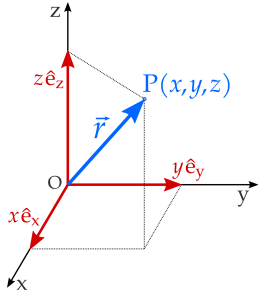
ভেক্টর রাশি সম্পর্কিত আরেকটা সংজ্ঞা হচ্ছে অবস্থান ভেক্টর। অবস্থান ভেক্টর নিয়ে জানার জন্য আমরা আবারও ত্রিমাত্রিক স্থানাংক ব্যবস্থা কে নিয়ে আসি যে ব্যবস্থায় একটা পয়েন্ট বা বিন্দু P হলে তার ত্রিমাত্রিক অবস্থান বা স্থানাংক হবে- P (x,y,z). যে ভেক্টর দিয়ে মূল বিন্দুর সাপেক্ষে ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থায় যেকোন বিন্দুর অবস্থান বের করা হয় তাকে অবস্থান ভেক্টর বলে। যদি মূল বিন্দু O এবং ত্রিমাত্রিক স্থানাংক ব্যবস্থায় যেকোনো বিন্দু P হয় তবে অবস্থান ভেক্টরটি হবে OP. অবস্থান ভেক্টরের আরেক নাম ব্যাসার্ধ ভেক্টর। তাই ছবি থেকে আমরা লিখতে পারি- OP = 𝒓⃗

শূন্য ভেক্টর (Null Vector)

যেসব ভেক্টরের মান এবং দিক কোনোটি নেই তাকে শূন্য ভেক্টর বলে। অথবা যেসব ভেক্টরের মান শূন্য তাকে শূন্য ভেক্টর বলে। শূন্য ভেক্টর কে প্রকাশ করা হয় 0 দিয়ে। তাই এই কয়েকটি ছিলো ভেক্টর রাশি সম্পর্কিত কিছু সংজ্ঞা।