ভেক্টর অভিক্ষেপ বোঝার জন্য একটা উদাহরণ দেই! তোমরা ঘরের মেঝের উপরে একটা লাঠিকে ঝুলিয়ে রাখো, তারপর সেই লাঠির উপরে লাইট জ্বালিয়ে দাও। দেখবে মেঝের উপরে লাঠির ছায়া পড়েছে। এই ছায়ার দৈর্ঘ্যকে বলা হয় ভূমির উপর লাঠির অভিক্ষেপ। তাই কোনো বস্তুর উপর অন্য বস্তুর ছায়াকে সেই বস্তুর অভিক্ষেপ বলে।

খেয়াল করো, লাঠি যদি বড় হয়, ছায়াও তত বড় হবে। তাই অভিক্ষেপ কিন্তু লাঠির দৈর্ঘ্যের উপর নির্ভর করে। আবার লাঠিকে তুমি যদি একটু বাকা করে দাও তবে লাঠির দৈর্ঘ্য আগের মত থাকার সত্ত্বেও মেঝেতে ছায়ার দৈর্ঘ্যও কম হবে। অর্থাৎ অভিক্ষেপ কমে যাবে। নিচের ছবিতে দেখো-

লাঠি যদি একদম ভূমি বা মেঝের সাথে লম্ব বরাবর থাকতো তবে আমরা একটা পয়েন্ট আকারে মেঝেতে অভিক্ষেপ দেখতে পেতাম। তাই লাঠি কিভাবে থাকছে তার উপরেও অভিক্ষেপ নির্ভর করে। অভিক্ষেপ নির্ভর করে-
- লাঠির দৈর্ঘ্যের উপর
- লাঠি কিভাবে আছে তার উপর
ভেক্টর অভিক্ষেপ বের করার নিয়ম
লাঠিকে যদি তুমি B ভেক্টর ধরো এবং মেঝেকে A ভেক্টর ধরো তবে B ভেক্টরের ছায়াকে বলা যায়- A ভেক্টরের উপর B ভেক্টরের অভিক্ষেপ
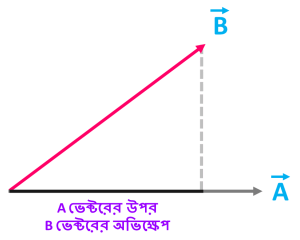
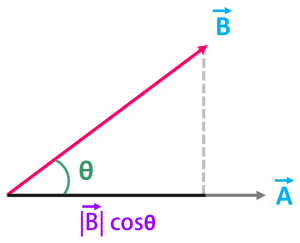
যদি লাঠি এবং অভিক্ষেপ এর মধ্যে θ কোণ কাজ করে তবে A ভেক্টরের উপর B ভেক্টরের অভিক্ষেপ হবে- |B| cosθ। যদি |B| cosθ বের করতে চাও তবে B ভেক্টরের শীর্ষবিন্দু থেকে A ভেক্টরের উপর লম্ব টানো। তখন A ভেক্টরের যতটুকু অংশ B এর অধীনে থাকবে সেটাই কিন্তু |B| cosθ. অর্থাৎ |B| cosθ হচ্ছে এক ধরনের ছায়া যেটা A এর উপর পরেছে।
ওদিকে আমরা উল্টোভাবে যদি A ভেক্টরের ছায়া B ভেক্টরের উপর ফেলি তবে A ভেক্টরের ছায়াকে বলা যায়- B ভেক্টরের উপর A ভেক্টরের অভিক্ষেপ।
নিচের ছবিতে দেখো-
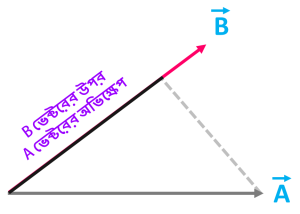
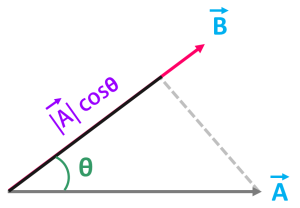
যদি ভেক্টর দুটোর মধ্যে θ কোণ কাজ করে তবে B ভেক্টরের উপর A ভেক্টরের অভিক্ষেপ হবে- |A| cosθ
আবার |A| cosθ বের করতে চাইলে A এর শীর্ষবিন্দু থেকে B ভেক্টরের উপর লম্ব টানো। তাহলে B ভেক্টরের যতটুকু অংশ A ভেক্টরের অধীনে থাকবে সেটাই |A| cosθ. অর্থাৎ |A| cosθ এক ধরনের ছায়া যেটা B এর উপর পরেছে।
এই ভেক্টর অভিক্ষেপ দুটোকে সংক্ষেপে ProjA এবং ProjB বলা হয়।
